∞
Disclaimer
This might be a challenging read as it delves into technical details, but I’ve made an effort to explain it as straightforwardly as I can. Despite its complexity and length, I believe this is one of the most captivating blog posts. I encourage you to read it in its entirety, as I find it to be quite exhilarating.
Introduction
I’ve just concluded watching an incredible documentary centered around the concept of infinity. Yet, it raises an initial question: what exactly is infinity? Is it a number, a concept, or perhaps a spatial or temporal domain? The answer, it seems, can vary depending on whom you ask. This leads to the subsequent inquiry: can we truly visualize infinity? Allow me to illustrate with a mathematical example.
\[ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} … + \frac{1}{2^{n}} = 1\]
If you sum an infinite sequence according to the provided equation, the result will always converge to one. For those familiar with Calculus, it’s evident that this represents a convergent series, where the addition of an infinite number of terms leads to a finite sum. Now, let’s examine its counterpart: divergent series. If we attempt to sum the following series, the result should be infinity:
\[ 1 + 2 + 3 + 4 … + n = \infty \]
Let’s take it a step further by bringing our sum and adding 1. We should get some sequence like this
\[ \infty + 1 = \infty \]
However, this is a paradox. Let me demonstrate why. If we were to subtract infinity from both sides now, we would get a famous mathematical expression:
\[ 1 = 0 \]
This might seem nonsensical. Many aspects within the realm of infinity lack practical comprehension and can frequently trigger existential contemplations. Hence, I found it intriguing to share some insights I acquired from this documentary that are truly mind-boggling! Brace yourself for a journey into the complexities of physics, permutations, and the profound nature of our existence.
The ∞ Hotel Paradox
Suppose we have a hotel that can fit an infinite amount of people. But first, this special hotel has some rules you should know before you proceed. The hotel is always full. However, there is also always space for new customers… So if a new customer wanted to stay the night at the hotel, everyone would move to room number \( n+1 \), where n is their current hotel number. Sounds easy enough, right? The next evening, an infinite number of people want an infinite number of rooms to stay in since the hotel always has free space. However the customers will not move \( n+ \infty \) rooms. Instead there is a even more clever solution: \( n * 2 \). So if you were in room 1, you would move to room 2, 2->4, 3->6, 4->8, and it goes on and on and on. What did you do? You freed up every odd hotel room, and now there are an infinite number of rooms for an infinite number of customers. Well done.
Some people have proposed that perhaps appending the new customers to \( \infty \) seems easier and must be more straightforward. However, the issue with this approach is that no one knows where the end of the hotel, aka room infinity, is. Therefore since it is not a finite quantity, this approach will never work. This leads us to the idea that not all infinities are the same, which we also learned in calculus. This idea of infinity is starting to become scary, and it’s only about to worsen.
∞ is small
Typically we think that infinity is a large quantity. However, let me demonstrate that infinity can also be a small quantity. How many numbers lie between 100 and 101? That’s right; it’s infinite. Suppose we visualize numbers like the data structure, stack. In that case, if we keep pushing on 0 to the top of our stack, there is an endless amount of quantities that lie between these numbers (i.e., 0.00001, 0.0000000000001,…). So how do we control infinity if it is both enormous and small?
Calculus
Calculus, often regarded as intricate and perplexing, didn’t rank among my favorite high school subjects. However, growing up has illuminated the fact that calculus serves as the language for comprehending change. Whether it involves motion, intricate systems, or even the mechanics of pandemics, calculus provides the framework to unravel their intricacies. So, if we adhere to our definition, we can harness the concept of infinity to elucidate the world’s workings. As mathematicians, we understand that something exists when we can observe it and confine it within a toolkit. That toolkit is calculus. Imagine we’re dealing with a curve that mirrors Earth’s orbit around the sun. We can conceptualize the orbit as an infinitely discretized arrangement of lines, resulting in an “orbital feature.” If we were to restrict our elliptical pattern to \( n = 5 \) lines, we’d obtain a jagged, pentagon-like path around the sun. Yet, with the boundlessness of this discretization, we can simulate any rotation or curve, all revolving around our constant of time. The beauty of this infinite discretization lies in its capacity to simplify complex systems. Consider a Fourier series [1], for instance. Essentially, it’s an endless sum of sines and cosines woven together to shape any conceivable waveform. By harnessing the Fourier series and the number of cycles required to traverse one iteration, mathematicians have woven an intricate tapestry of various series to craft images using these Fourier components… a feat that’s truly awe-inspiring.
What I’m attempting to convey here is that this “bird artist” concept is essentially a intricate fusion of mathematical series, all layered atop each other. However, by dissecting each series into its constituent parts, mathematicians could ingeniously decode the art of drawing birds using vectors! This approach of deconstructing simple systems to decipher more intricate ones is a monumental practice in fields like systems biology and electrical engineering. Given our brain’s finite capacity, we’re compelled to devise ways of comprehending expansive systems in more manageable terms. This progression from simplicity to complexity has heralded numerous groundbreaking revelations. Among them stands electricity, a transformative force that has redefined our world.
Where to find ∞
I’ve endeavored to provide a glimpse into the visualization of infinity. However, these concepts inevitably steer us toward a more profound question: Does infinity hold a place within our physical reality? The answer to that inquiry oscillates between both affirmation and negation.
Due to its inherent attributes, physicists often liken black holes to a tangible manifestation of infinity. But what precisely is a black hole? At its core, it’s an immensely dense void that engulfs matter so completely that nothing manages to escape its gravitational clutches. This is why our knowledge about these enigmatic entities remains profoundly limited. The film “Interstellar” adeptly portrays the visualization of these systems; physicists attest to its fairly accurate depiction. Within this portrayal lies the mesmerizing event horizon, as vividly depicted in the accompanying GIF below.
How precisely do black holes exhibit similarities to infinity? We’ll employ Einstein’s theory of relativity to delve into a theoretical explanation of this correlation and unveil the inner workings of a black hole. According to Einstein, venturing into a black hole equates to an experience of infinite falling, even though this plummeting sensation is inherently finite. Einstein’s conjecture posits that at a certain juncture, you’ll encounter the “floor” of the black hole, known as the singularity—a point of infinite curvature in space-time where all the mass of the black hole converges. In this realm, density becomes infinite, yielding a cataclysmic environment. The intensity is so profound that it triggers a rupture in the fabric of physics, rendering you imperceptible. Essentially, you cease to exist. I’ll refrain from delving deeper into this explanation since the known world essentially shatters within a black hole’s domain, obviating the need for further queries, according to Einstein.
However, a faction of physicists declines to embrace Einstein’s postulate and instead entertains the notion that a black hole constitutes a wormhole. A wormhole entails two temporally distant points connected by a funnel-like structure, permitting near-instantaneous traversal between these points. I say “near-instantaneous” because certain elements within our universe aren’t infinite. One such parameter is speed, which tops out at 299,792,458 meters per second—the speed of light—signifying an unattainable velocity threshold. Consequently, even if two points were separated by billions of light-years, their connectedness would still be confined by the speed of light’s constraints.
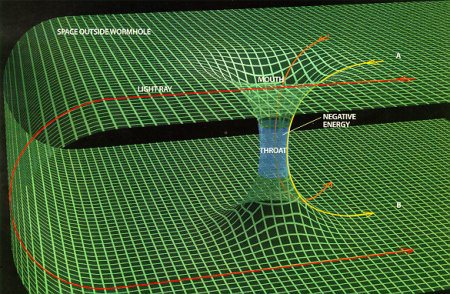 |
|---|
| Visual of the wormhole: distant spatial points connected by a funnel |
This leads us to an exhilarating exploration of the concept of infinite time. Does time stretch infinitely? What would be the fate of an object existing throughout infinite time? This brings us to a captivating thought experiment involving an object encased within a box. Imagine placing an orange inside the box. Over the course of ten days, it might succumb to decay; over a span of 100 years, it could potentially disintegrate into microscopic particles due to bacterial activity. Yet, governed by the laws of thermodynamics, the energy and atoms within this orange would traverse the box, transitioning between various forms. Given a fixed size for the orange, the atoms could potentially adopt around \( 10^{10^{24}} \) distinct configurations. While this number is staggeringly immense, there will come a juncture when the orange exhausts the available permutations it can assume. Thus, after an infinite expanse of time, the hypothesis posits that upon opening the box, we’d discover the orange, ideally in a pristine, healthy state, lying there on its own.
This idea of having finite solutions within an observable space leads us to our universe.
Parallel Universes
Space is widely believed to stretch into infinity. However, what we can observe, or the limited number of galaxies within our knowledge, comprises a finite-dimensional space. Let’s envision this finite-dimensional space as an amalgamation of minuscule cubic voxels. Within this framework, our “universe” is composed of a definite quantity of these voxels. Suppose certain states or orientations define our universe’s potential configurations. This notion sets a cap on the variety of permutations our universe can adopt. Hence, within the confines of our known finite dimensions (observable space), there exists a boundary on the potential appearances of our universe.
Now, things start to venture into the realm of mind-bending possibilities. Consider the scenario where there exist copies of our universe’s orientation, situated at a distance beyond our reach. This inaccessibility stems from the previously established limit that speed cannot surpass 299,792,458 meters per second. These distant copies might be merely a few billion years away, which is essentially too far for us to traverse. However, within this realm of infinity, emerges the intriguing notion of parallel universes. Could it be that these parallel universes encompass an infinite array of diverse decisions unfolding concurrently over infinite time? Envision our lives as intricate decision trees, each branch representing a choice made or not made. In this model, imagine querying our crush; how might such a decision reverberate through the subsequent sequences of events?
 |
|---|
| Video Game Decision Trees that can resemble decision trees in our own lives |
Think of it like the enigmatic time stone featured in “Avengers: Infinity War.” Through this lens, we can glimpse how infinite permutations unfold within the tapestry of our own lives. The astonishing concept is that these countless decision pathways likely run in parallel at some distant spatial juncture—an absolutely mind-bending notion. Yet, we remain unable to catch a glimpse of ourselves in a parallel universe, where we’re either millionaires or reincarnated as sheep, for the simple reason that we don’t share proximity with these parallel realms where our infinite selves exist in infinite spatial points. A bit of a bummer, isn’t it?
Now, for those who might still harbor doubts regarding the speed limit governing the universe, allow me to illustrate the supremacy of the speed of light with another example. Consider the stars that grace our night sky; they appear minuscule because they reside billions of light years away from Earth. Each time we cast our gaze upon these stars, we’re essentially peering into the past. Why? Because the light from these stars embarked on a billion-year journey across the cosmos to reach us. Consequently, by the time their light reaches our eyes, these celestial bodies have likely journeyed even farther away in the vast expanse of space. Isn’t it incredible? Each shimmering point in the night sky carries the echo of its past, a celestial projection of where the star, comet, or planet was eons ago. This phenomenon is a direct consequence of light’s steadfast pace, maintaining a constant velocity of 299,792,458 meters per second. This cosmic speed limit is what delayed our perception of these celestial spectacles until their distant light finally graced our eyes.
 |
|---|
| A hand-drawn drawing of what our eyes perceive when we see planet X, in this case, |
Just a Spec in the Universe
Now that we’re acquainted with the undeniable supremacy of light’s speed in our universe, and even that speed is deemed insufficiently swift, where does that leave us? In a universe that might be infinite, why should we invest our efforts in exploring potentially habitable exoplanets? As someone who once championed space exploration fervently in their youth, I can’t help but wonder if these ventures might prove futile, particularly if the target planets aren’t within practical reach—say, within our own solar system. Yet, even within our cosmic neighborhood, the likes of Mars or Jupiter’s moon, Europa, remain formidable challenges to reach, demanding an investment of time that might ultimately lack worthwhile returns.
This disillusionment with the grandeur of space exploration and our hopes for interplanetary habitation raises a pressing question: Does any of this truly matter? Amidst all the irreversible harm humanity has inflicted upon our own planet, what have we genuinely done to safeguard Mother Earth? In contrast, we’re but fleeting specks within this infinite expanse, each individual’s existence confined to a painfully brief and finite time interval. So, what are we striving to achieve during our transient stay on this cosmic stage? This is the point where excessive contemplation can spiral into an existential abyss. Logically dissected, life appears devoid of inherent purpose, yet humans possess the remarkable ability to inject meaning into a seemingly purposeless existence.
As intricate as our world may be, human beings are no less complex, with emotions holding particular sway over our lives. My personal stance is influenced by these emotions—love, anger, joy—and they seemingly infuse life with its vibrancy. The concept of whether love is boundless (infinite) piques my interest. Could love be an observable infinity in our tangible reality? I’d like to believe it is, but I must ponder whether it’s possible to sustain unwavering love for someone throughout an entire lifetime. During my relatively short journey, I’ve maintained profound connections with a few individuals, harboring the desire to love them indefinitely. However, the question of whether love’s infinity holds true seems to be a matter of subjectivity. From my vantage point, only time will reveal the answer.
Returning to the theoretical realm, let’s contemplate the notion of unending movement in a single direction. Analogous to Earth, physicists propose that our universe possesses a spherical shape. If we were to journey continuously in one direction for eternity, we’d eventually find ourselves back where we began. However, physicists also posit that the universe’s shape is expanding at an accelerating pace, causing galaxies to drift apart. This insight holds little immediate significance for us, but within the broader framework of conceivable spatial domains, it might suggest that the timeline for life in the universe is finite. While the universe itself will endure, the existence of life as we know it could wane (predicted within 100 billion years). Life, it seems, mirrors our own temporality, occupying a brief interval that won’t extend infinitely. This juxtaposition renders life’s history remarkably brief against the backdrop of boundless infinity.
So what
The reality is that this concern should hold no universal importance. A significant portion of theoretical physics and mathematics is pursued solely to unravel the enigmas of our cosmos. As I conclude, I’d like to present a final contemplation: Are humans themselves infinite entities? Could an unending diversity of human forms persist for the next 100 billion years? The probable response is a resounding no, but gauging humans against this yardstick is rendered complex by the constraints of their fleeting lifetimes. My trajectory toward this assertion is influenced by a parallel with the observable universe; akin to the universe’s limits, our cognitive capacities are confined by the boundaries of neuron capacity. These neurons intricately weave into an exponential array of configurations, yet even this expansive spectrum is undoubtedly finite. Hence, considering all the discussions explored in this blog post, I posit that due to the inherent limitations in the permutations of our cognitive faculties, humans themselves cannot lay claim to the quality of infinity.
This leads me full circle to a final inquiry: What, then, truly constitutes infinity?
Footnote
[1] Fourier Series - an infinite series of trigonometric functions representing an expansion or approximation of a periodic function.
